Lecture 9 - Hypothesis Tests

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
import scipy

torch.manual_seed(42)

<torch._C.Generator at 0x112a1c3f0>

Two-Sample Test

We have two potential titles for a Youtube video. We want to see which one has a higher click-through-rate.

• Title A: 98 views over 1000 impressions

• Title B: 162 views over 2000 impressions

We conduct a permutation test to test whether CTR for A (\theta_A) is equal to CTR for B (\theta_B).

H_0: \theta_A=\theta_B, \quad H_1: \theta_A \neq \theta_B.

Our test statistic is |\hat{\theta}_A-\hat{\theta}_B|.

my_viewsA = 98 # number of clicks for video A
my_viewsB = 162 # number of clicks for video B

n_impsA = 1000 # number of impressions for video A (total number of people who saw video title)
n_impsB = 2000 # number of impresssion for video B

Dataset A: (1, \dots, 1, 0, 0, \dots, 0) (98 ones, 902 zeros)

Dataset B: (1,\dots, 1, 0, \dots, 0) (162 ones, 1838 zeros)

my_viewsA/n_impsA

0.098

my_viewsB/n_impsB

0.081

obs_T = abs(my_viewsA/n_impsA - my_viewsB/n_impsB) # |theta_1 - theta_2|

obs_T

0.017

We pool the Dataset A and Dataset B. (We will shuffle Dataset A and Dataset B in the permutation test).

all_views = my_viewsA + my_viewsB
all_imps = n_impsA + n_impsB
pool = np.array([1]*all_views + [0]*(all_imps - all_views))

Here is an example of a random draw from the null distribution (that the CTR of A and B is the same).

# Sample without replacement for impsA
impsA = np.random.choice(pool, n_impsA, replace=False)
# new permuted dataset of size n_impsA
viewsA = np.sum(impsA)
viewsB = all_views - viewsA

Permutation test:

• draw 500 samples from null distribution
• for each sample s=1,\dots, 500, calculate T_s = |\hat{\theta}_{A, s}-\hat{\theta}_{B, s}|
• locate actual observed T_{obs}=|\hat{\theta}_A-\hat{\theta}_B| in sample distribution: \text{p-val} = \frac{1}{S}\sum_{s=1}^{500} \mathbb{1}(T_s\geq T_{obs} )

n_perm = 500
resampled_Ts = np.zeros(n_perm) # where to store our permutation test statistics

for cur_sim in range(n_perm):
    # Pool with 1s for views and 0s for non-views
    pool = np.array([1]*all_views + [0]*(all_imps - all_views))
    # create an array with (98+162) ones and (1000+2000 - 98-162) zeros
    
    # (1, 1, 1, 1, ..., 1, 0, 0, 0, ..., 0) (1, 1,.., 1, 0, 0, 0, 0, ...,0)
    # (1, 1, 0, 0, 0, 1, ..., 0, 1, 0, )

    # Sample without replacement for impsA
    impsA = np.random.choice(pool, n_impsA, replace=False)
    # new permuted dataset of size n_impsA
    viewsA = np.sum(impsA)
    viewsB = all_views - viewsA
    
    resampled_Ts[cur_sim] = abs(viewsA/n_impsA - viewsB/n_impsB) # | theta_1 -theta_2| for this dataset

p_value = sum([1 for t in resampled_Ts if t >= obs_T]) / n_perm

print(f"P-Value: {p_value:.4f}")

plt.hist(resampled_Ts, bins=20)
plt.axvline(obs_T, color='red')
plt.show()

P-Value: 0.1140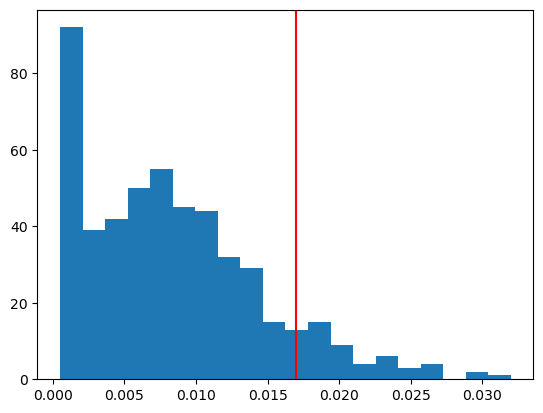

Conclusion: we retain the null hypothesis.

Independence test with neural networks

Data: (X_1,Y_1), (X_2, Y_2),\dots, (X_n, Y_n)

We consider two different methods to conduct an independence test:

H_0: X \text{ is independent of } Y \text{ vs. } H_1: X, Y \text{ not independent}

Method 1

• Generate 500 random permutations (X_1, Y_{\pi(1)}),\dots, (X_n, Y_{\pi(n)})
• For each permutation:
  • Split into train/test
  • Train neural network on train data
  • Calculate error on test data (T_s)
• For actual data:
  • Split into train/test
  • Train neural network on train data
  • Calculate error on test data (T_{obs})
• Calculate p-value: \text{p-val} = \frac{1}{S}\sum_{s=1}^{500} \mathbb{1}(T_s\geq T_{obs} )

class NNet(nn.Module):
    def __init__(self, in_dim, out_dim):
        super(NNet, self).__init__()
        self.sequential = nn.Sequential(
            nn.Linear(in_dim, 2*in_dim),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(2*in_dim, out_dim))

    def forward(self, x):
        return self.sequential(x)

We create simulated data which we know is NOT independent.

Ideally, we should reject the null hypothesis that Y and X are independent.

p1 = 5 # dimension of X
p2 = 3 # dimension of Y

signal_strength = 0.3

n_samples = 10000

X = np.random.randn(n_samples, p1)

B = np.random.randn(p2, p1)
B = B / np.linalg.norm(B, ord='fro') # some parameter

Y = signal_strength * X @ B.T + np.random.randn(n_samples, p2)
# Y = B X + random noise

X = torch.tensor(X, dtype=torch.float32)
Y = torch.tensor(Y, dtype=torch.float32)

def testerr(x, y, epochs=200):

    # trains a neural network to predict y from x
    ntrain = int(n_samples * 0.7) # train on 70% of the data
    ntest = n_samples - ntrain

    x_train = x[:ntrain]
    x_test = x[ntrain:]

    y_train = y[:ntrain]
    y_test = y[ntrain:]

    net = NNet(p1, p2)
    net.train()
    optimizer = optim.Adam(net.parameters(), lr=0.2)
    for epoch in range(epochs):
        optimizer.zero_grad()
        outputs = net(x_train)
        
        loss = nn.MSELoss(reduction='mean')(outputs, y_train)
        loss.backward()
        optimizer.step()
    
    net.eval()
    outputs = net(x_test)
    loss = nn.MSELoss(reduction='mean')(outputs, y_test)

    return loss.item()

# our observed test statistic is the loss in predicting y from x
obs_T = testerr(X, Y)

obs_T

1.0054599046707153

# Perform permutation testing
n_permutations = 500
resampled_Ts = []

for _ in range(n_permutations):
    permuted_Y = Y[torch.randperm(n_samples)]
    resampled_T = testerr(X, permuted_Y) # train a neural network, output training loss
    resampled_Ts.append(resampled_T)

# Calculate p-value
p_value = sum([1 for t in resampled_Ts if t <= obs_T]) / n_permutations

# plot distribution of permuted_test_statistics
plt.hist(resampled_Ts, bins=20)
plt.axvline(obs_T, color='red')
plt.show()


print(f"Observed test statistic: {obs_T:.4f}")
print(f"P-Value: {p_value:.4f}")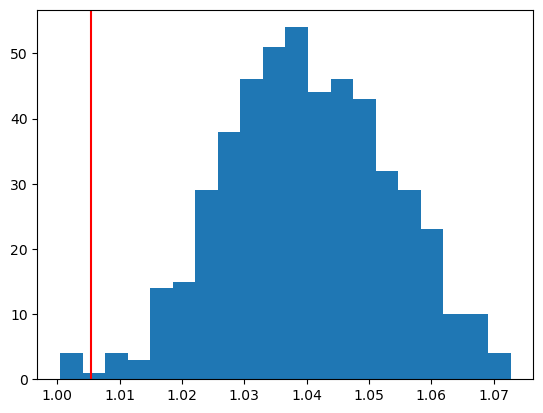

Observed test statistic: 1.0055
P-Value: 0.0080

Method 2

• Split into train and test data
• Train f to predict Y from X
• Train baseline f_{base} to predict Y (this is \bar{Y})
• For each datapoint, compute error: z_i = Loss(f(x_i), y_i),\quad \widetilde{z}_i=Loss(f_{base}, y_i)
• For s=1,\dots, 500:
  • Switch z_i and \widetilde{z}_i with probability 0.5
  • Calculate mean(z_{i,s}) - mean(\widetilde{z}_{i,s})
• For observed data:
  • Calculate mean(z_i) - mean(\widetilde{z}_i)
• Calculate p-value

## sample split
ntrain = int(n_samples * 0.7) # train on 70% of the data
ntest = n_samples - ntrain

X_train = X[:ntrain]
X_test = X[ntrain:]

Y_train = Y[:ntrain]
Y_test = Y[ntrain:]

net = NNet(p1, p2)

net.train()
epochs = 200
optimizer = optim.Adam(net.parameters(), lr=.2)
for epoch in range(epochs):
    optimizer.zero_grad()
    outputs = net(X_train)
        
    loss = nn.MSELoss(reduction='mean')(outputs, Y_train)
    loss.backward()
    optimizer.step()

net.eval()
testerrs = torch.sum((Y_test - net(X_test))**2, dim=1)
mean_testerr = torch.mean(testerrs)

testerrs

tensor([0.6410, 0.7331, 6.1261,  ..., 4.2328, 1.2628, 4.6177],
       grad_fn=<SumBackward1>)

nullerrs = torch.sum((Y_test - torch.mean(Y_train, dim=0))**2, dim=1)
mean_nullerr = torch.mean( nullerrs )

nullerrs

tensor([0.7893, 0.7796, 5.9333,  ..., 4.5801, 1.6773, 4.4518])

print(f"Mean Test Errors: {mean_testerr:.4f}")
print(f"Mean Null Test Errors: {mean_nullerr:.4f}")

obs_T = mean_testerr - mean_nullerr

Mean Test Errors: 3.0165
Mean Null Test Errors: 3.0656

combined = torch.stack((testerrs, nullerrs), dim=1)

heads = torch.randint(0, 2, (ntest,))

resampled_testerrs = combined[torch.arange(ntest), heads]
resampled_nullerrs = combined[torch.arange(ntest), 1-heads]

n_permutations = 500
resampled_Ts = []

for _ in range(n_permutations):
    heads = torch.randint(0, 2, (ntest,))

    resampled_testerrs = combined[torch.arange(ntest), heads]
    resampled_nullerrs = combined[torch.arange(ntest), 1-heads]
    # test error using X - test error not using X
    resampled_T = torch.mean(resampled_testerrs) - torch.mean(resampled_nullerrs)
    resampled_Ts.append(resampled_T)

## Calculate p-value
p_value = sum([1 for t in resampled_Ts if t <= obs_T]) / n_permutations

resampled_Ts = [t.detach().numpy() for t in resampled_Ts]
plt.hist(resampled_Ts, bins=20)
plt.axvline(obs_T.detach().numpy(), color='red')
plt.show()

print(f"P-Value: {p_value:.4f}")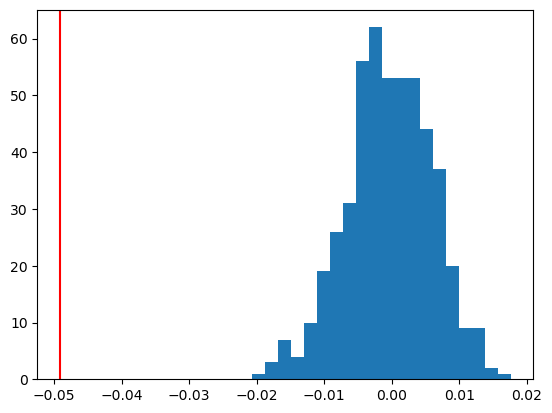

P-Value: 0.0000