Lecture 2b - Supervised Learning

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

np.random.seed(1)

import warnings
warnings.filterwarnings('ignore')

Data

We consider the Kings County housing dataset. It includes homes sold between May 2014 and May 2015.

Specifically, we focuse on the Rainier Valley zipcode.

# Load the dataset
house = pd.read_csv("data/rainier_valley_house.csv")

Here are the features:

house.columns

Index(['Unnamed: 0', 'id', 'date', 'price', 'bedrooms', 'bathrooms',
       'sqft_living', 'sqft_lot', 'floors', 'waterfront', 'view', 'condition',
       'grade', 'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated',
       'zipcode', 'lat', 'long', 'sqft_living15', 'sqft_lot15'],
      dtype='object')

# number of houses
print(f"number of houses:  {house.shape[0]}")

plt.boxplot(house['price'])
plt.title('Price Boxplot')
# make plot small in jupyter output
plt.gcf().set_size_inches(4, 3)

plt.show()

number of houses:  508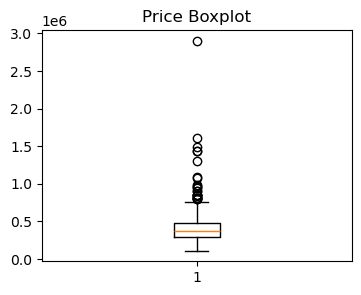

## For houses with 0, 1, 2, ... bedrooms, show their median price
print(house.groupby('bedrooms')['price'].median().reset_index())

   bedrooms     price
0         0  228000.0
1         1  299000.0
2         2  325000.0
3         3  365000.0
4         4  447500.0
5         5  425000.0
6         6  462500.0
7         7  370500.0

# Filtering houses priced under 1 million
house = house[house['price'] < 1e6]

## Plot year built vs. price
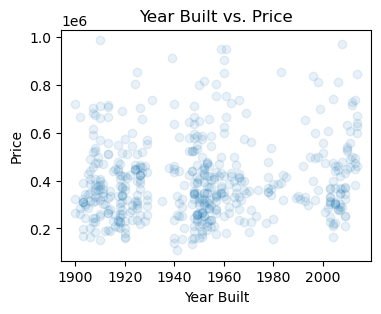
plt.scatter(house['yr_built'], house['price'], alpha=0.1)
plt.xlabel('Year Built')
plt.ylabel('Price')
plt.title('Year Built vs. Price')
plt.gcf().set_size_inches(4, 3)
plt.show()

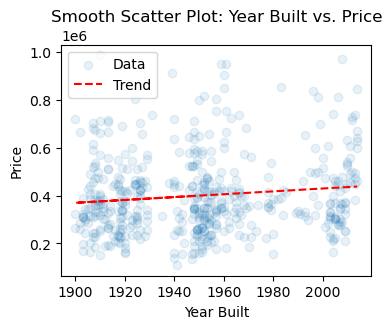
## Smooth scatter plot of year built vs. price
plt.scatter(house['yr_built'], house['price'], alpha=0.1, label='Data')
z = np.polyfit(house['yr_built'], house['price'], 1)
p = np.poly1d(z)
plt.plot(house['yr_built'], p(house['yr_built']), "r--", label='Trend')
plt.xlabel('Year Built')
plt.ylabel('Price')
plt.title('Smooth Scatter Plot: Year Built vs. Price')
plt.legend()
plt.gcf().set_size_inches(4, 3)
plt.show()

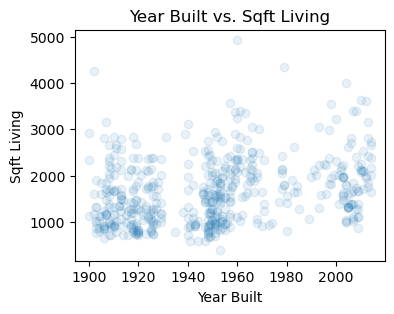
## Plot year built vs. sqft_living
plt.scatter(house['yr_built'], house['sqft_living'], alpha=0.1)
plt.xlabel('Year Built')
plt.ylabel('Sqft Living')
plt.title('Year Built vs. Sqft Living')
plt.gcf().set_size_inches(4, 3)
plt.show()


## Pairwise plot of price, bedrooms, and sqft_living
#pd.plotting.scatter_matrix(house[['price', 'bedrooms', 'sqft_living']], alpha=0.1, figsize=(10, 10))
#plt.show()

## Group by condition and calculate mean price
print(house.groupby('condition')['price'].mean().reset_index())

   condition          price
0          1  227000.000000
1          2  246749.705882
2          3  396841.120482
3          4  420201.384615
4          5  433258.152174

plt.figure(figsize=(10, 8))
sc = plt.scatter(house['long'], house['lat'], c=house['price'], cmap='viridis', alpha=0.5)
plt.colorbar(sc, label='Price ($)')
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.title('House Location and Price')
plt.gcf().set_size_inches(5, 4)
plt.show()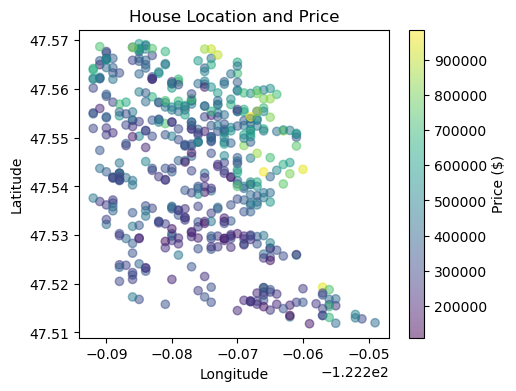

K-Nearest Neighbors

# We will consider this subset of features
features = ["floors", "grade", "condition", "view", "sqft_living",
            "sqft_lot", "sqft_basement", "yr_built", "yr_renovated",
            "bedrooms", "bathrooms", "lat", "long"]

Y = house['price'] / 1000
X = house[features]

## Standardize the features
scaler = StandardScaler()
X_stan = scaler.fit_transform(X)

## Split the data into training and test sets
n_train = 400
n_test = 100

idx = np.random.permutation(len(Y))
X_stan = X_stan[idx]
Y = Y.iloc[idx]

X_train = X_stan[:n_train]
X_test = X_stan[n_train:(n_train + n_test)]
Y_train = Y[:n_train]
Y_test = Y[n_train:n_train + n_test]

## Implement KNN
K = 7
Y_pred = []

for test_point in X_test:
    distances = np.sqrt(((X_train - test_point)**2).sum(axis=1))
    nearest_neighbors_indices = distances.argsort()[:K]
    Y_pred.append(Y_train.iloc[nearest_neighbors_indices].mean())

Y_pred = np.array(Y_pred)
Y_pred_baseline = Y_train.mean()

# Evaluate test error
test_error = np.sqrt(((Y_test - Y_pred) ** 2).mean())
baseline_error = np.sqrt(((Y_test - Y_pred_baseline) ** 2).mean())
print(f"Test RMSE of KNN: {test_error:.3f}   Baseline RMSE: {baseline_error:.3f}")

#print test R-squared
R2 = 1 - test_error**2 / baseline_error**2
print(f"Test R-squared of KNN: {R2:.3f}")

Test RMSE of KNN: 243.110   Baseline RMSE: 333.415
Test R-squared of KNN: 0.468

from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor

# Split the data into training and test sets
X_train, X_test, Y_train, Y_test = train_test_split(X_stan, Y, test_size=100, train_size=400, random_state=1)

all_errs = []

for K in range(1, 30):
    knn = KNeighborsRegressor(n_neighbors=K)
    knn.fit(X_train, Y_train)
    Y_pred = knn.predict(X_test)

    # Evaluate test error
    test_error = np.sqrt(((Y_test - Y_pred) ** 2).mean())
    all_errs.append(test_error)

plt.plot(range(1, 30), all_errs, marker='o')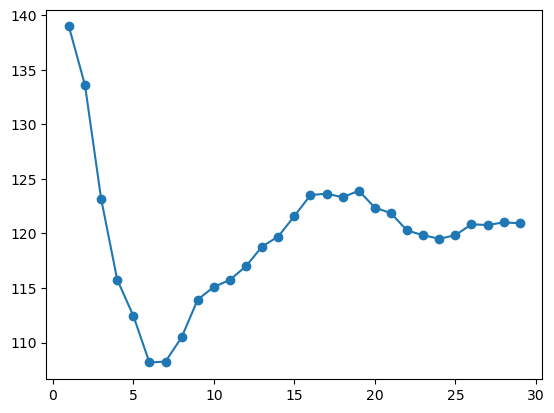

Linear regression

## linear regression
X_stan1 = np.hstack([np.ones((X_stan.shape[0], 1)), X_stan])
X_train, X_test, Y_train, Y_test = train_test_split(X_stan1, Y, test_size=100, train_size=400, random_state=2)

betahat = np.linalg.solve(X_train.T @ X_train, X_train.T @ Y_train)
Y_pred = X_test @ betahat

test_error = np.sqrt(((Y_test - Y_pred) ** 2).mean())
baseline_error = np.sqrt(((Y_test - Y_train.mean()) ** 2).mean())

## print coefficients
print("Coefficients:")
features = X.columns
for i, f in enumerate(features):
    print(f"{f}: {betahat[i]:.3f}")


print(f"Test RMSE of linear regression: {test_error:.3f}   Baseline RMSE: {baseline_error:.3f}")

R2 = 1 - test_error**2 / baseline_error**2
print(f"Test R-squared of linear regression: {R2:.3f}")

Coefficients:
floors: 416.418
grade: 12.421
condition: 58.902
view: 18.317
sqft_living: 44.802
sqft_lot: 87.841
sqft_basement: 87.671
yr_built: -17.770
yr_renovated: -9.817
bedrooms: 6.158
bathrooms: -33.250
lat: 9.441
long: 72.392
Test RMSE of linear regression: 94.613   Baseline RMSE: 195.243
Test R-squared of linear regression: 0.765

## use sklearn to do linear regression
from sklearn.linear_model import LinearRegression

linreg = LinearRegression()
linreg.fit(X_train, Y_train)
Y_pred = linreg.predict(X_test)

test_error = np.sqrt(((Y_test - Y_pred) ** 2).mean())
baseline_error = np.sqrt(((Y_test - Y_train.mean()) ** 2).mean())

print(f"Test RMSE of linear regression: {test_error:.3f}   Baseline RMSE: {baseline_error:.3f}")

R2 = 1 - test_error**2 / baseline_error**2
print(f"Test R-squared of linear regression: {R2:.3f}")

Test RMSE of linear regression: 94.613   Baseline RMSE: 195.243
Test R-squared of linear regression: 0.765